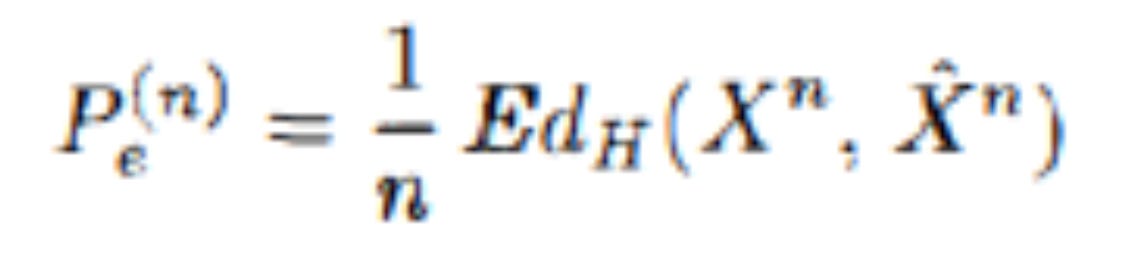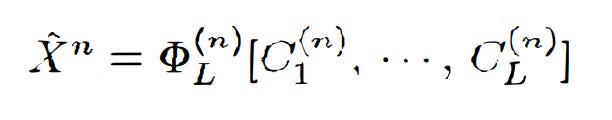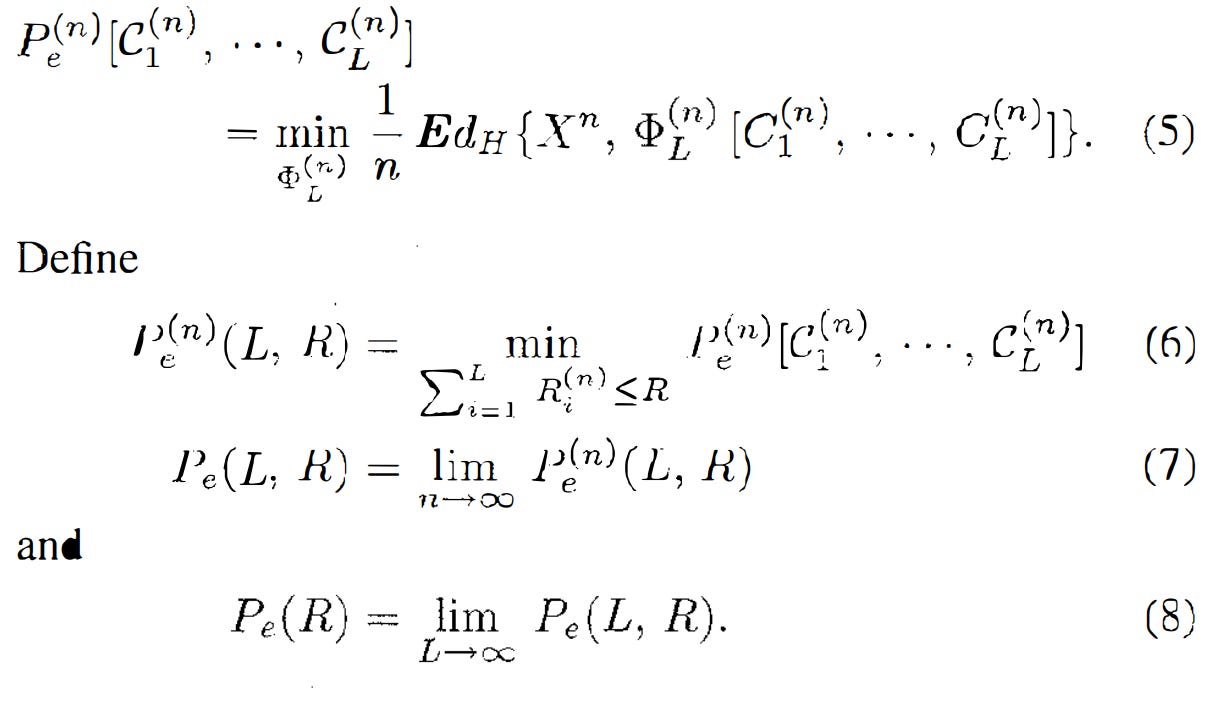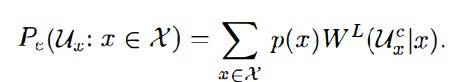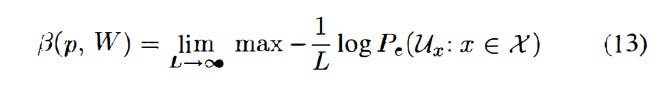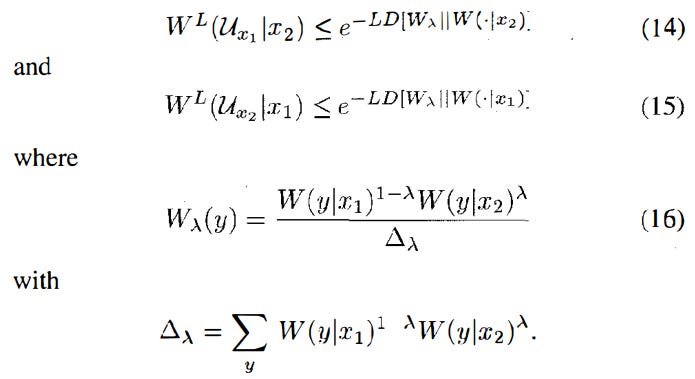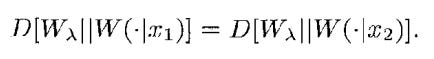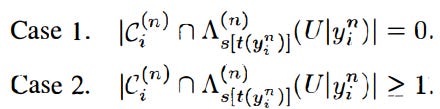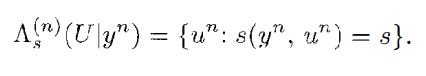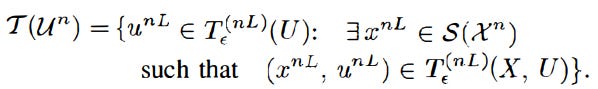The CEO Problem
CEO's have a hard time listening to everyone; how could they find minimal distortion from the input from multiple agents?
Imagine a Fortune 500 CEO, extremely busy managing many assets and departments, getting a report of a certain important message they need to address. However, since the CEO is very busy, they cannot look at the message directly. So, they deploy a number L of the company’s representative agents to look at the message and report back. Due to the nature of the message (say it was a cryptographic one or an international one with multiple translations or one under high-security clearance), each agent has a distorted view of the whole problem message. Each of the L agents observes the message independently, and can only report back to the CEO in R bits per second since the CEO is very busy.
Let D be the distortion, i.e. the amount of change/error the message received by the CEO is compared to the ground truth message. If the agents were allowed to converse beforehand, then with the limit of L → inf, they should be able to smooth out their independent observation noises (distortions and errors) and send the info to the CEO with a fidelity of D(R) ← distortion rate. If R exceeds the entropy rate (H(X(t))), then D can be made arbitrarily small. The entropy (H(x)) of message X(t) at time t represents how much of the signal information is transmitted and how much uncertainty there is about the signal over time, at time t.
However, say that the agents cannot convene before reporting to the CEO, there is no finite value of R which even infinitely many agents (L→ inf) can make D arbitrarily small. In this isolated agent case, measuring the Hamming distortion, there can be an asymptotic behavior of the minimum achievable D as L and R → inf.
This problem is called the CEO problem in information theory. Here, the CEO can also mean “Centralized Encoder and Optimizer,” a central node that decodes coded information from peripheral information sources. The problem was formalized in this paper by Berger, Zhang, and Viswanathan in 1996, and has since been a staple in discussion about multiterminal source coding. Their definition of the CEO problem is also commonly mentioned as the Gaussian CEO Problem, as it assumes the data follows a multivariate Gaussian distribution. Even though there is no provable and defined solution, there are many theorems and derivations branching from the problem as fit to other scenarios and distributions.
Taking a step back, multiterminal source coding is a branch of information theory that deals with the compression and collection of multiple correlated information sources that are not fully independent (they have some sort of statistical, informational, or dependence relationship). The primary objective of the field of study is to efficiently compress the sources while preserving relevant information. One could think of this as an adjacent study to quantization, feature dropping, and regularization in machine learning.
One of the earlier problems in the area was the Slepian-Wolf coding problem, which is a method of theoretically coding two lossless compressed correlated sources. Given two statistically dependent independent and identically distributed (i.i.d) finite alphabet random sequences (i.i.d. means each variable is statistically independent of others and they follow the same probability distribution), the theorem gives a theoretical bound for lossless coding rate for distributed coding of two sources. With joint decoding, as long as the total rate of X and Y is larger than their joint entropy H(X, Y), none of the sources is encoded with a rate smaller than its entropy. This allows the coding to create an arbitrarily small error probability. Often, the distortion is measured through Hamming distance - the # of positions between two strings of equal length at which the symbols are different in corresponding locations. Also, to define another term, code blocks are often a measure/representation of segments of data that are being encoded/decoded by the system, usually comprised of a fixed number of bits/size of a matrix.
Let’s formalize the problem!
The problem isn’t really useful without mathematical formalization; I won’t go through all of the theorems or proofs, but we can take a walk through the main relevant math formalization which is a basis for many other papers on remote source coding. Substack’s latex block is still finicky, so you’ll have fun reading these representations:
L: number of agents
X(t), t in [1, inf): the data sequence message
D(.): distortion rate function of X(t)
Y_i(t): the noisy observations from agent i
p(x): probability distribution common to the random variables of X (the message in the domain of possible messages)
C_i(n): the source code
c_i(n): code word
x^n: recovered message
X^n: the CEO’s estimate of the random message (with caret, ground truth without caret)
d_H: Hamming distance
n: code block size
The CEO’s job is to recover the source message with a small expected symbol error frequency:
The CEO has a mapping (cumulative distribution function) of all of the source codes from i to L, which maps to X^n, for this purpose. Therefore, the CEO’s estimate is defined as:
It is noted that although C_i(n) is a codeword selected by agent i, since the distribution is random, C_i(n) is effectively random.
The main goal of the CEO problem is to study the tradeoff between the total rate of the encoders and the minimum achievable expected error frequency.
Pulling straight from the paper:
We see that the minimum achievable error is calculated by finding the min of the expected value of the Hamming distance between the ground truth and the cumulative distribution function of the code words, which will eventually occur with the limit of L and R to inf.
The paper then shows multiple theorems of the relation; first, the error cannot be 0 except for certain degenerate pairs. For nondegenerate problems, increasing R will decay Pe(R) exponentially, but still not hitting 0.
Definition: Degenerate means that the probability mass is concentrated on a single outcome (problems are trivial or a single solution), while nondegenerate means that the probability mass is spread across multiple outcomes (problems are nontrivial, possibly having multiple solutions). A degenerate pair usually refers to a pair of sequences or events in which one of the sequences is completely predictable or redundant when given the other sequence.
This means that even as L → inf and if the code blocks could be arbitrarily long (effectively piling a lot of information per channel), the agents will still pay a penalty for not being able to have a data-pooling consensus before informing the CEO. I won’t go through the derivation/proof here (as it is mostly equations in the paper), but in short, the authors min the KL divergence (D_kl(P||Q), the measure of statistical distance; how one probability P is different from a second, reference, probability distribution Q) as R → inf.
There are some other theorems that the authors go over in the paper, such as the problem without the coding element. This happens when n is set to 1
The problem is then reformatted as: Let X be a finite alphabet, p(x) be a distribution on X with each x in X. With each x, there’s a distribution W(.|x) on the set of Y. The task is to decide which of these distributions is in force (relevant and applicable). W(.|x) is the true common distribution of the random variables. We want to minimize
which effectively means we’re solving the max problem:
U_x is a decision rule that distinguishes between two x’s. The authors note that for any decision rule (Ux1, Ux2) that is optimal for distinguishing between W(.|x1) and W(.|x2), there is a lambda where 0≤lambda≤1 such that
When the problem is to minimize the sum of two kinds of error probabilities, we should take a lambda such that
Then you can prove the result, which is B(p, W) = min(D[Wlambda||W(.|x1)]). This may seem like a lot of math, but it essentially creates a simplified problem of how to find the decision rule parameters.
Random Coding Method
The entire workflow for the CEO Problem the authors propose is:
Random Code Structure:
The codes C_i(n) are constructed using a random variable satisfying the mapping X→Y→U, where the probability of U given Y is equal to the Q function of a variable u in U given y in Y. According to the probability distribution, then we will select M codewords from Un independently. Given the distribution is probably normal, this is where the name Gaussian CEO Problem comes from.
Encoding Rule
When Agent i is faced with encoding an observed sequence y_i(n), there are two cases:
where
in case 1, the agent sends the symbol 0 to the CEO. In Case 2, the agent sends the index of the box that contains one element from the set. Each of the L agents uses the same rate in the scheme. Also, as L → inf, the rate of each agent can be kept small even if the total rate is allowed to grow; this means each agent can remain illicit if needed.
Decoding Rule
If the CEO receives a 0, an error is declared. Otherwise, the CEO attempts to recover the true codewords from the specified boxes of codewords. Let B = b1 x b2 x … bL be the cartesian product of boxes whose indices have been specified. For any xn in Xn, consider mapping S: Xn→XnL which repeats the source word xn, L times; this gives us: S(Xn) = US(xn), S(xn) = (xn, … xn) in XnL. Defining S(Xn) as the union of all S(xn), and also
if |T(Un) and B| ≠ 1, there is a decoding error. Else, if the only element of the set is the super codeword (a primary method of recovering information), the recovered code words are un1, ….unL
Estimation Rule
There may be more than one xnL that is jointly typical (pairs that are statistically related). So, the authors estimate the data componentwise, similar to the decision rule. Take the sum of the product of the true distribution of y given x, with the prob that u given x would obtain a value beyond a certain standard deviation threshold, and choose the UxL that maximizes the product of it * the probability of x. This creates a decision region for each word xn in Xn, and then if a decoding rule produces a super code word that belongs to its U, the estimate is xn.
Error Probability
There are a couple of error probability methods, including the encoding error probability (probability that case 1 occurs at one or more of the encoders), decoding error probability, and error frequency estimates
The CEO problem overall has many applications; one of which is in the reign of federated learning (FL), such as in this paper. Federated learning is a method of training a model across multiple decentralized devices/servers while keeping the data localized. This preserves privacy and reduces the need to share sensitive/large datasets centrally; 3rd party training systems, gov-cloud systems, and volunteer compute systems largely use this model. Every time the model weight is updated, this is a CEO problem across training nodes with the central weight vector; therefore, the goal is to obtain the minimum achievable rate at a particular upper bound of gradient variance. Other similar systems include the BOINC volunteer computer system.
The CEO problem is a very interesting open problem in information theory, growing increasingly important as the scalability and modularity of ML and information processing spread today.